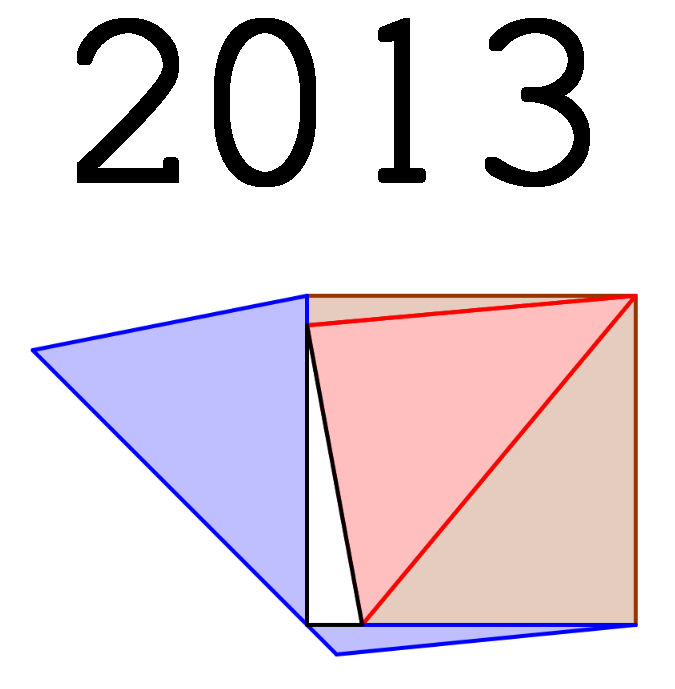
Eine geometrische Zahlenspielerei zum Jahr 2013
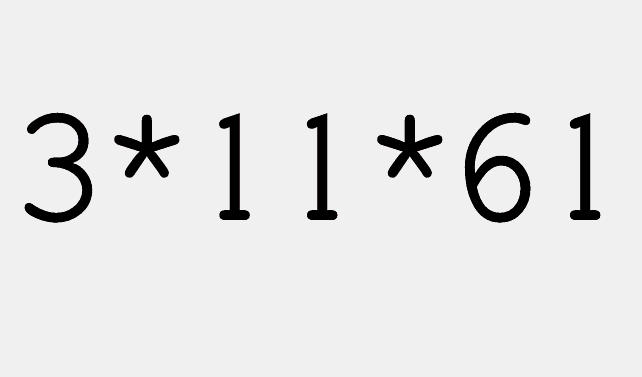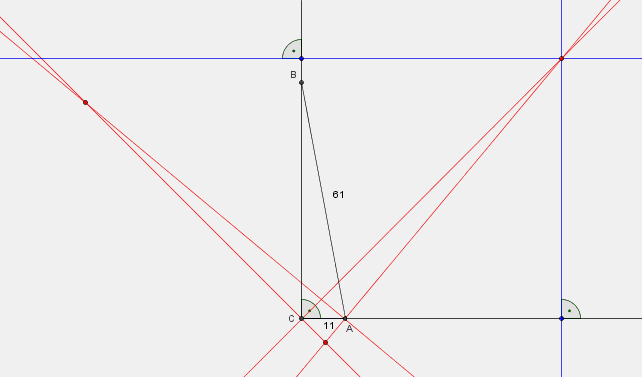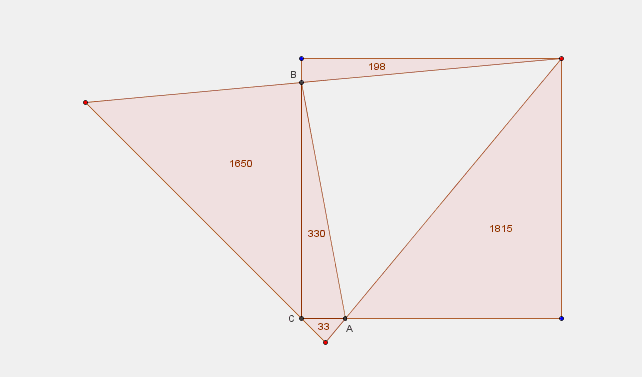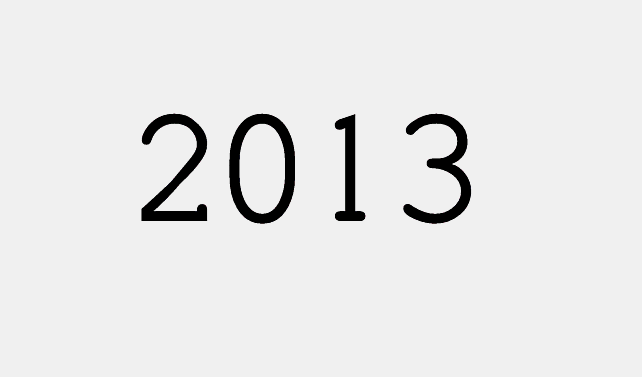
Konstruktionsdetails
Berechnung
Primitive pythagoreische Tripel die zu drei ganzzahlig gleichgroßen Flächen führen.
| n |
b = 4*(n-1)+3 |
c = (2*n-1)^2+(2*n)^2 |
a = sqrt(c^2-b^2) |
drei gleichgroße Flächen n*b*c |
| 1 |
3 |
5 |
4 |
15 |
| 2 |
7 |
25 |
24 |
350 |
| 3 |
11 |
61 |
60 |
2013 |
| 4 |
15 |
113 |
112 |
6780 |
| 5 |
19 |
181 |
180 |
17195 |
| 6 |
23 |
265 |
264 |
36570 |
| 7 |
27 |
365 |
364 |
68985 |
| 8 |
31 |
481 |
480 |
119288 |
| 9 |
35 |
613 |
612 |
193095 |
| ... |
... |
... |
... |
... |
Feststellungen zu rechtwinkligen Dreiecken:
1.) Die Hypotenuse halbiert die Fläche eines aus den Mittelpunkten der Ankreise gebildeten Dreiecks.
2.) Die Fläche eines rechtwinkligen Dreiecks ist gleich dem Produkt:
a) aus Hypotenusenankreisradius und Inkreisradius;
b) der Kathetenankreisradien.
3.) Die Hypotenuse ist gleich:
a) der Summe der Kathetenankreisradien;
b) dem Radius des Kreises auf dem die Mittelpunkte der Ankreise liegen.
4.) Der Hypotenusenankreisradius ist gleich der Summe:
a) der Dreiecksseiten geteilt durch zwei;
b) von Hypotenuse und Inkreisradius;
c) von Ankathete und Gegenkathetenankreisradius;
d) von Gegenkathete und Ankathetenankreisradius.
5.) Der Abstand der Kathetenankreismittelpunkte ist gleich der Länge der Diagonalen des Hypotenusenquadrates.
6.) Der Inkreismittelpunkt und der Hypotenusenankreismittelpunkt liegen einander gegenüber auf dem Umkreis des Hypotenusenquadrates.
Zeichnungen erstellt mit
GeoGebra
Besuchen sie auch die Webseiten von
Prof. Dr.-Ing. habil. Jürgen Dankert
dem Erfinder der
Jahreszahlen-Spielereien
Karl Hovekamp, Dezember 2012
Letzte Ergänzung: 21. Januar 2014
Kontakt: karl(at)hovekamp.info

